Mejlholm, O. and Dalgaard, P. (2007b). Modeling and predicting the growth of lactic acid bacteria in lightly preserved seafood and their inhibiting effect on Listeria monocytogenes  J. Food Prot. 70 (11), 2485-2497.

Mejlholm, O., Bøknæs, N., Dalgaard, P. (2014). Development and evaluation of a stochastic model for potential growth of Listeria monocytogenes in naturally contaminated lightly preserved seafood. Food Microbiol. http://dx.doi.org/10.1016/j.fm.2014.06.006

Mejlholm, O., Dalgaard, P. (2015). Modelling the simultaneous growth of Listeria monocytogenes and lactic acid bacteria in seafood and mayonnaise-based seafood salads. Food Microbiol. http://dx.doi.org/10.1016/j.fm.2014.07.005

This model includes the effect of 12 environmental parameters (See Table above) on the simultaneous growth of L. monocytogenes and lactic acid bacteria (LAB) in lightly preserved seafood including many ready-to-eat products. Information on the lag time of L. monocytogenes in naturally contaminated lightly preserved seafood is still limited. Therefore, the growth model for L. monocytogenes can be used without lag time (fail safe predictions) or with lag time (more realistic predictions for naturally contaminated products). FSSP uses a relative lag time of 4.5 for L. monocytogenes. This lag time option is not available for LAB because numerous studies have confirmed these bacteria to grow without a significant lag time in lightly preserved seafood. See the FSSP dialog box and output window below (Fig. 1).

FSSP predicts how high concentrations of LAB dampen and stops the growth of L. monocytogenes. This Jameson effect is most imporetant to accuratelty predict concentrations of L. monocytogenes and their influence on food safety. As shown in Fig. 1 and Fig. 2 the FSSP software allow these predictions to be carried out conveniently for constant and variable temperature storage conditions.

Fig. 1. The graph above shows the predicted growth of L. monocytogenes and LAB for vacuum-packed cold-smoked salmon. Predictions are shown for two products with different smoke intensity (5 or 15 ppm phenol) and without or with added acetic acid. As shown FSSP predicts the time needed for the concentrations of L. monocytogenes and LAB to increase 100-fold under the selected product characteristics and storage conditions. The concentrations of L. monocytogenes and LAB shown in the bar at the bottom of the output window was obtained by using the mouse to click on the graph at a specific point in time.

Fig. 2. Effect of two simple temperature profiles on the predicted simultaneous growth of L. monocytogenes and LAB.

Primary growth model

The Logistic model with delay and including interaction between L. monocytogenes and LAB is shown in Eqn. 1 below. The primary growth model describes how the specific growth rates of L. monocytogenes ([dLm/dt]/Lm_t) and of lactic acid bacteria ([dLAB/dt]/LAB_t) are reduced when the cell concentrations of the two bacteria (Lm_t and LAB_t, cfu g^-1) approaches their maximum values (Lm_max and LAB_max cfu g^-1). The model is an expansion of the differential form of the simple Logistic model. Eqn. 1 with γ = 1.0 includes the assumption that LAB inhibit growth of L. monocytogenes to the same extend that they inhibit their own growth. This has been confirmed for various lightly preserved seafoods and FSSP therefore uses eqn .1 with  γ = 1 as the default value. However, in some situations growth of L. monocytogenes may continue to increase or sometimes decrease after LAB reaches their maximum population density. By using values of γ (also called the 'competition factor' or the 'Inhibiting effect factor of LAB on L.m.') bewteen 0 and 2 FSSP allows these growth patterns to be predicted (Fig. 3).

Eqn. 1. Primary model for simultaneous growth of Listeria monocytogenes and LAB. t_lag-Lm is the lag time for L. monocytogenes. Other model parameters are described in the text above the equation.

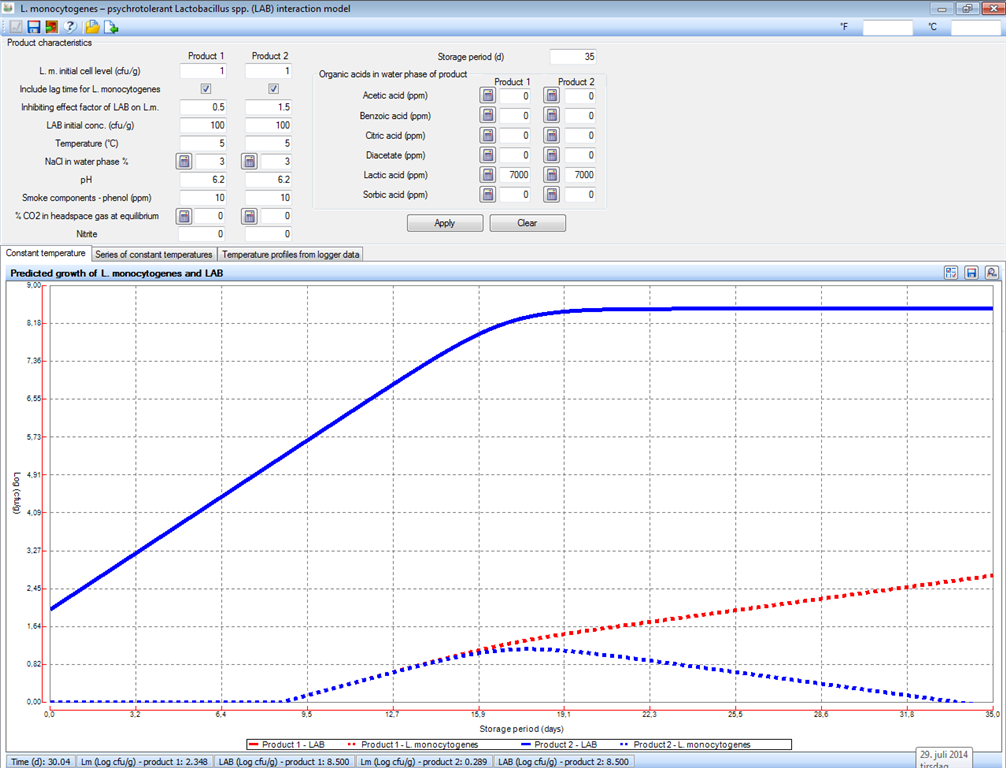
Fig. 3. Examples of how values of 0.5 and 1.5 for the competition factor (γ) influence the inhibiting effect of LAB on the predicted growth of L. monocytogenes.

Secondary growth and growth boundary model:

Eqn. 2a and Eqn. 2b  below show the secondary growth models for L. monocytogenes and lactic acid bacteria. These simplified cardinal parameter type models describe how the maximum specific growth rate  (µ_max, h^-1) at a reference temperature of 25°C (µ_max-ref) is reduced when environmental parameters become less favourable for growth. The term for each of the environmental parameters (temperature, water activity (water phase salt), pH, phenol (smoke components), CO₂ (atmosphere) and undissociated organic acids) all has a value between 0 and 1. FSSP predicts the growth boundary of L. monocytogenes as the combination of environmental conditions resulting in µ_max = 0 and a specific term (ξ) is included in the cardinal parameter models to take into account the effect of interaction between all the different environmental parameters (Eqn. 2). Like other terms in the secondary model 'ξ' has a value between 0 and 1 (Eqn. 3). With temperature (T), undissociated lactic acid (LAC_U) and undissociated diacetate (DAC_U) as examples, Eqn. 3, 4 and 5 show how the value of the interaction term (ξ) is calculated. This approach to predict the growth boundary was first suggested by Yvan Le Marc and colleagues (Le Marc et al. 2002). Later, various studies have found the Le Marc-approach valuable for growth boundary modelling (Mejlholm & Dalgaard, 2007a,b; Mejlholm & Dalgaard, 2009).

Listeria monocytogenes secondary model (Eqn. 2a)

Evaluation and validation of the Listeria monocytogenes and lactic acid bacteria models: 

The models included in FSSP for prediction of the simultaneous growth of L. monocytogenes and LAB have been evaluated by comparison of observed and predicted growth in inoculated challenge tests and in naturally contaminated products as shown in the Table below. The models performed very well and bias factors for both models were within the ranges for successful model validation of 0.87 < Bias factor < 1.43 for L. monocytogenes (Ross, 1999) and 0.85 < Bias factor < 1.25 for LAB  (Mejlholm and Dalgaard, 2013).